A few weeks ago, I facilitated a session at the Teachers Development Group Leadership Seminar to support teachers in creating conditions that naturally invite productive and interesting conjectures in secondary mathematics classrooms. Though much of intellectual progress in mathematics and the sciences has relied on our ability to question and/or extend conventional wisdom, students often feel bound by convention and find themselves pursuing others’ mathematical questions rather than their own. The process of making and exploring conjectures — claims and problems we pose for ourselves — affords students an environment to question, use and refute “established” knowledge as appropriate, and reason from fundamental principles rather than abstractions that may feel removed from personal experiences.
For enduring change, shifting the culture for students requires a shift in collaborative teacher learning. So I posed the wonderment – to what extent are teachers being encouraged to make and test their mathematical questions such that they are afforded the opportunity to make and grow mathematics themselves? For participants in the session, the goal was to dip their toes into the world of making and testing conjectures by taking a closer look into the Functions domain they teach.
I posed the following questions.
- Are there more lines than points in the 2D space?
To test their initial conjectures, among other pathways, some participants —
Plotted a line in the m-b plane (slope-y-intercept plane).
Made a list/table of at least 5 points on this line.
Since each of these points in the m-b plane represents a line in the x-y plane, they used the Desmos calculator to plot these lines.
With noticings from these steps, they were able to think more deeply about their initial claims but no one arrived at an “answer” to the question they’d want to stand behind!
**I didn’t provide the solution to give folks a bit more time to wrestle, but for those of you who’ve continue to ponder — here it is.
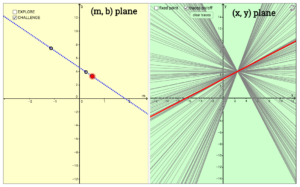
Looking at the graphical representations, a point in the m-b plane corresponds to a line in the x-y plane. It turned out that a line in the m-b plane also corresponds to a point in the x-y plane. This is the point around which all the lines in the x-y plane (that came from the points along the line in the m-b plane) rotates. That sounds confusing…
Let’s work it out.
Cardinality of the set of Points in 2D plane?
–A point in the 2D in the Cartesian plane is defined by its x and y coordinates.
–Since both x and y coordinates are numbers on the real number line, ℝ, this means that there are n(ℝ)2 possible points in the 2D plane (product of x and y).
Cardinality of the set of Lines in 2D plane
— Many Lines can be represented by the equation y = mx + b
— Since both m and b coordinates are numbers on the real number line, ℝ, this means that there are n(ℝ)2 lines in the form y = mx + b in the 2D plane (again, product of m and b).
— But not all lines are captured by the slope intercept form. There are vertical lines of the form x = r where r is also a number on the real number line. Therefore, the cardinality of vertical lines is n(ℝ).
—> Putting this together, the total amount of lines in the 2D plane is n(ℝ)2 + n(ℝ).
So what does this mean? Infinite sets are always a head scratcher, but we now pull on the fact that
n(ℝ)2 + n(ℝ) = n(ℝ)2 = n(ℝ) = n(ℝ)3 = n(ℝ)k for any natural number k
(http://math.stackexchange.com/questions/183361/examples-of-bijective-map-from-mathbbr3-rightarrow-mathbbr)
Ergo, the sets of lines, n(ℝ)2 + n(ℝ), and points, n(ℝ)2, are equal.
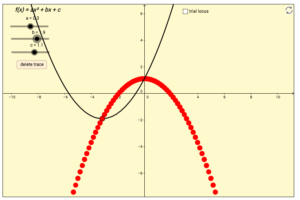
2. We know how varying the parameters ‘a’ and ‘c’ affect the form of the graph of a quadratic function, but what is the impact of varying the parameter ‘b’? What is the equation of the parabola that’s traced by the vertex of a quadratic function for fixed values of ‘a’ and ‘c’ while the parameter ‘b’ is varied?
3. What happens when you trace a square instead of a unit circle? What are the “trig” functions and identities that come out of this exercise?